CÁC HÀM SỐ LƯỢNG GIÁC – TOÁN LỚP 11
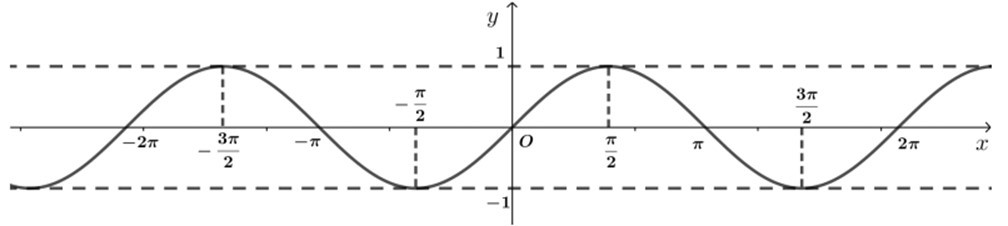
- Hàm số sin.
– Định nghĩa:
Quy tắc đặt tương ứng mỗi số thực x đối với số thực sin x
sin: R → R
x → y = sin x
được gọi là hàm số sin, kí hiệu là: y = sinx.
– Tập xác định của hàm số sin là R.
– Tập giá trị : G = [–1; 1] có nghĩa là -1 ≤ sinx ≤ 1 ∀x ∈ R
– Là hàm số lẻ.
– hàm số y = sin x là hàm số tuần hoàn với chu kì 2π.
– Tính đơn điệu:
Hàm số đồng biến trên mỗi khoảng (-π/2+k2π; π/2+k2π) và nghịch biến trên mỗi khoảng (π/2+k2π; 3π/2+k2π)
– Vì y = sin x là hàm số lẻ nên đồ thị hàm số đối xứng qua gốc tọa độ O.
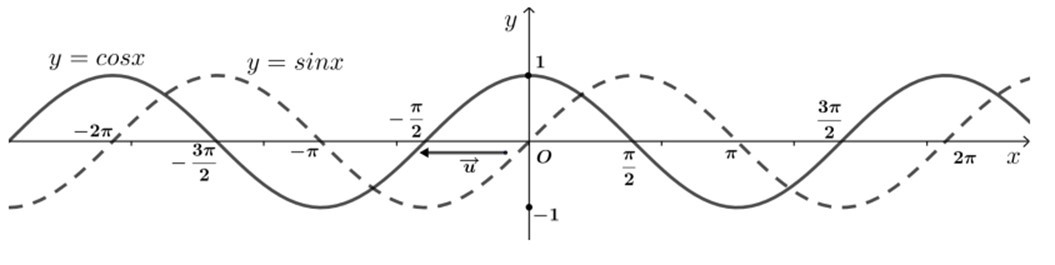
2. Hàm số cosin
– Định nghĩa:
Quy tắc đặt tương ứng mỗi số thực x đối với số thực cos x
cos: R → R
x → y = cos x
được gọi là hàm số cosin, kí hiệu là: y = cos x.
– Tập xác định của hàm số cosin là R.
– Tập giá trị : G = [–1; 1] có nghĩa là -1 ≤ sinx ≤ 1 ∀x ∈ R
– Là hàm số chẵn
– hàm số y = cos x là hàm số tuần hoàn với chu kì 2π.
– Tính đơn điệu:
Hàm số đồng biến trên mỗi khoảng (-π+k2π; k2π) và nghịch biến trên mỗi khoảng (k2π; π+k2π)
– Vì y = cos x là hàm số chẵn nên đồ thị hàm số đối xứng qua trục tung.
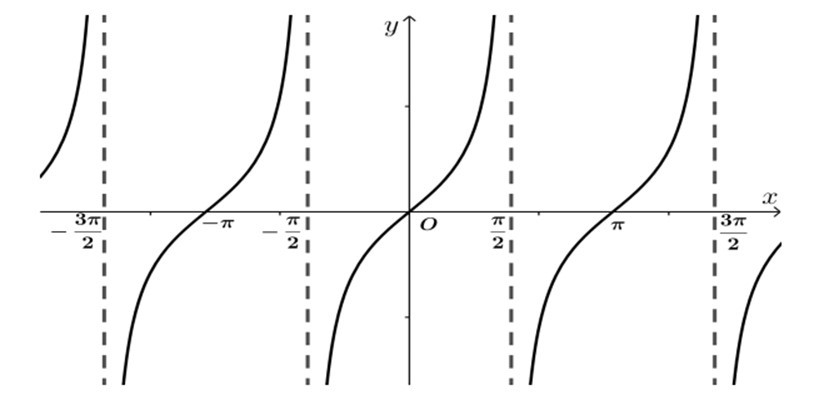
3. Hàm số tang
– Định nghĩa: Hàm số tang là hàm số được xác định bới công thức: (cos x ≠ 0)
– Kí hiệu là y = tan x
– Tập xác định của hàm số y = tan x là D = R\{π/2 + kπ, k ∈ Z}.
– Tập giá trị của hàm số y = tan x là khoảng (–∞; +∞)
– Là hàm số lẻ.
– Hàm số y = tan x là hàm số tuần hoàn với chu kì π
– Hàm số y = tan x đồng biến trên (-π/2+kπ; π/2+kπ) ; (k ∈ Z)
– Đồ thị hàm số có tâm đối xứng là gốc tọa độ O
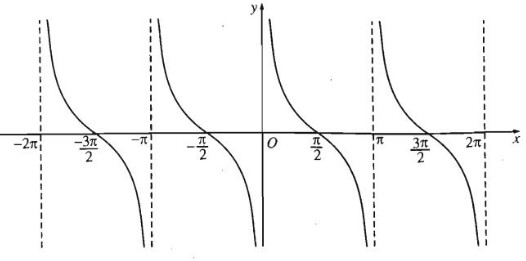
4. hàm số cotang
– Định nghĩa:
Hàm số cotang là hàm số được xác định bới công thức: (sin x ≠ 0)
– Kí hiệu là y = cot x
– Tập xác định của hàm số y = cot x là D = R\{kπ, k ∈ Z}.
– Tập giá trị của hàm số y = cot x là khoảng (–∞; +∞)
– Là hàm số lẻ.
– Hàm số y = cot x là hàm số tuần hoàn với chu kì π
– Hàm số y = cot x nghịch biến trên khoảng (kπ; π+kπ) ; (k ∈ Z)
– Đồ thị hàm số có tâm đối xứng là gốc tọa độ O