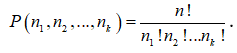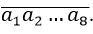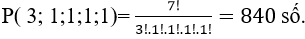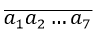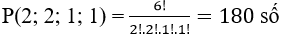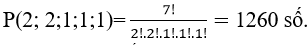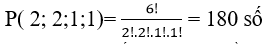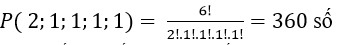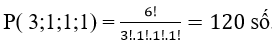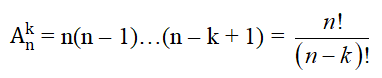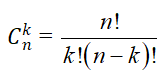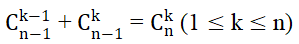Hoán vị, chỉnh hợp, tổ hợp

                                                      HOÁN VỊ, CHỈNH HỢP, TỔ HỢP – TOÁN 11

I. HOÁN VỊ

1. Định nghĩa hoán vị:

Cho tập hợp A, gồm n phần tử (n>=1). Một cách sắp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.

Công thức hoán vị:

$P_n=n(n-1)(n-2)...2.1=n!$

Ví dụ:

Tính số cách xếp $6$ bạn học sinh thành một hàng dọc.

Hướng dẫn:

Mỗi cách xếp $6$ bạn học sinh thành một hàng dọc là một hoán vị của $6$ phần tử.

Vậy số cách xếp $6$ bạn học sinh thành một hàng dọc là $P_6=6!=720$.

2. Hoán vị lặp :

Cho n phần tử, trong đó có n₁ phần tử x₁ , n₂ phần tử x₂, …, n_k phần tử x_k

(n₁+n₂+…+n_k=n). Mỗi cách sắp xếp n phần tử đó vào n vị trí gọi là một hoán vị lặp của n phần tử đã cho.

Số tất cả các hoán vị lặp của n phần tử ở trên là :

Ví dụ 1 : Từ tập X={1;2;3;4;5;6;7;8} lập được bao nhiêu số tự nhiên có 11 chữ số sao cho chữ số 1 có mặt 4 lần, các chữ số khác có mặt 1 lần?

A.11!/4!    B.11!    C.11!/4    D. 4.11!

Hướng dẫn giải :

Đáp án : A

Mỗi cách lập số có 11 chữ số sao cho chữ số 1 có mặt 4 lần, các chữ số khác có mặt 1lần là một hoán vị lặp của 11 phần tử .( số 1 xuất hiện 4 lần; các số khác 1 lần).

Theo quy tắc hoán vị lặp có tất cả số các số thỏa mãn là:

Ví dụ 2 : Với các chữ số 0; 1;2; 3; 7; 9 có thể lập được bao nhiêu số gồm 8 chữ số, trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng một lần?

A.6720 số    B.40320 số    C.5880 số    D.840số

Hướng dẫn giải :

Đáp án : C

Gọi số có 8 chữ số là: 

+ Mỗi cách lập số có 8 chữ số sao cho chữ số 1 xuất hiện 3 lần và các số khác có mặt xuất hiện 1 lần là một hoán vị lặp của 8 phần tử ( số 1 xuất hiện 3 lần; các số khác xuất hiện 1 lần).( tính cả trường hợp a1 = 0).

Theo quy tắc hoán vị lặp có tất cả:

+ Xét trường hợp a1= 0.

Ta tính số các số có 7 chữ số được lập từ các chữ số 1;2;3;7;9 trong đó chữ số 1 có mặt 3 lần; các chữ số khác có mặt đúng 1 lần.

Theo quy tắc hoán vị lặp có tất cả:

Suy ra số các số thỏa mãn đề bài là: 6720 – 840= 5880 số.

Ví dụ 3 : Từ các số của tập A= { 2; 4; 6; 8} lập được bao nhiêu số tự nhiên gồm bảy chữ số, trong đó chữ số 2 xuất hiện đúng hai lần; chữ số 4 xuất hiện 2 lần; chữ số 6 xuất hiện 2 lần và chữ số 8 xuất hiện 1 lần.

A.312    B.302    C.320    D.630

Hướng dẫn giải :

Đáp án : D

+ Mỗi cách lập số có 7 chữ số thỏa mãn: chữ số 2 xuất hiện đúng hai lần; chữ số 4 xuất hiện 2 lần; chữ số 6 xuất hiện 2 lần và chữ số 8 xuất hiện 1 lần là một hoán vị lặp của 7 phần tử .

+ Theo quy tắc hoán vị lặp có tất cả:

Ví dụ 4 : Cho tập A= { 1; 3; 5; 6; 9}. Từ tập A ta lập được bao nhiêu số có 7 chữ số sao cho chữ số 1 xuất hiện 2 lần; chữ số 6 xuất hiện 2 lần; các số khác xuất hiện đúng 1 lần và số này chia hết cho 5.

A.360    B.540    C.180    D.1260

Hướng dẫn giải :

Đáp án : C

Gọi số có 7 chữ số thỏa mãn đầu bài là: 

+ Do số này chia hết cho 5 nên ₇ = 5.

+ Bài toán trở thành tính số các số có 6 chữ số được tạo ra từ tập { 1; 3; 6; 9} sao cho chữ số 1 xuất hiện 2 lần; chữ số 6 xuất hiện 2 lần và 3; 9 chỉ xuất hiện 1 lần.

Theo quy tắc hoán vị lặp có:

Suy ra có 180 số thỏa mãn bài toán

Ví dụ 5 : Từ tập X= {1; 2; 4; 6; 7; 9}. Từ tập X ta lập được bao nhiêu số có 8 chữ số sao cho chữ số 4 xuất hiện 2 lần; chữ số 2 xuất hiện 2 lần; các chữ số khác xuất hiện đúng 1 lần và số đó không chia hết cho 2.

A.3780    B.2890    C.3620    D.4260

Hướng dẫn giải :

Đáp án : A

Gọi số thỏa mãn bài toán là: 

+ Vì số này không chia hết cho 2 nên a₈≠{1; 7; 9}.

+ Trường hợp 1. Nếu a₈= 1. Bài toán trở thành tính số các số có 7 chữ số sao cho chữ số 4 xuất hiện 2 lần; chữ số 2 xuất hiện 2 lần; các số 6; 7; 9 xuất hiện 1 lần.

Theo quy tắc hoán vị lặp có:

+ Tương tự; nếu a₈ = 7; 9 ta cũng có 1260 số thỏa mãn.

Suy ra: số các số thỏa mãn đầu bài là:

1260+ 1260+ 1260= 3780 số.

Ví dụ 6 : Cho tập X={1; 2; 5; 6; 8}. Hỏi từ tập X lập được bao nhiêu số có 7 chữ số trong đó chữ số 8 xuất hiện 2 lần; chữ số 6 xuất hiện 2 lần; các số khác xuất hiện đúng 1 lần và số đó chia hết cho 5.

A.180     B.360    C.540    D.720

Hướng dẫn giải :

Đáp án : A

Gọi số có 7 chữ số thỏa mãn đầu bài là: 

+ Do số cần lập chia hết cho 5 nên a₇= 5.

+ Khi đó; số các số thỏa mãn đầu bài bằng số các số có 6 chữ số sao cho chữ số 8 xuất hiện 2 lần; chữ số 6 xuất hiện 2 lần;các số 1, 2 xuất hiện đúng 1 lần.

+ Theo quy tắc hoán vị lặp; số các số thỏa mãn là:

Vậy có 180 số thỏa mãn đầu bài.

Ví dụ 7 : Cho tập A= {2; 4; 5; 6; 7}. Hỏi từ tập A lập được bao nhiêu số có 7 chữ số sao cho chữ số 4 xuất hiện 2 lần; chữ số 5 xuất hiện 2 lần; các số khác xuất hiện đúng 1 lần và số đó chia 2 thì dư 1.

A.280    B.360    C.540    D.720

Hướng dẫn giải :

Đáp án : C

Gọi số có 7 chữ số thỏa mãn đầu bài là : 

+ Do số cần lập chia cho 2 thì dư 1 nên số cần lập là số lẻ.

⇒ a₇ ≠ { 5; 7}.

+ Trường hợp 1. Nếu a₇ = 5.

Ta tính số các số có 6 chữ số trong đó chữ số 4 xuất hiện 2 lần; các chữ số 2; 5; 6; 7 xuất hiện đúng 1 lần

Theo quy tắc hoán vị lặp có:

+ Trường hợp 2.Nếu a₇= 7.

Ta tính số các số có 6 chữ số sao cho chữ số 4 xuất hiện 2 lần; chữ số 5 xuất hiện 2 lần; các số 4 và 6 xuất hiện đúng 1 lần

Theo quy tắc hoán vị lặp có:

Kết hợp hai trường hợp suy ra số các số thỏa mãn đầu bài là:

360+ 180= 540 số

Ví dụ 8 : Cho tập X= {0;1; 3;5;6}. Từ tập X ta lập được bao nhiêu số có 7 chữ số sao cho chữ số 1 xuất hiện 3 lần; các số khác xuất hiện đúng 1 lần và số đó vừa chia hết cho 2 vừa chia hết cho 5.

A. 240    C. 360     C. 150    D.120

Hướng dẫn giải :

Đáp án : 120

Gọi số có 7 chữ số thỏa mãn đầu bài là: : 

Do số cần tìm vừa chia hết cho 2 vừa chia hết cho 5 nên số đó chia hết cho 10.

⇒ a₇= 0.

Khi đó; số các số thỏa mãn đầu bài chính là số các số có 6 chữ số sao cho chữ số 1 xuất hiện 3 lần; các số 3,5,6 xuất hiện đúng 1 lần.

Theo quy tắc hoán vị lặp ta có:

Vậy có 120 số thỏa mãn đầu bài.

3. HOÁN VỊ VÒNG QUANH:

Định nghĩa: Cho tập hợp X gồm n phần tử. Mỗi cách sắp xếp n phần của X trên một đường tròn gọi là một hoán vị vòng quanh của n phần tử của tập X.

Các cách sắp xếp các phần tử của X trên một đường tròn mà sai khác nhau một phép quay được coi là cùng một hoán vị vòng quanh.

Số các hoán vị vòng quanh của n phần tử khác nhau được tính bởi công thức: Q_n=(n-1)!

Ví dụ 1 : Tổ 1 của lớp 10A1 có 4 học sinh nữ và 6 học sinh nam .Hỏi có bao nhiêu cách xếp các học sinh này vào một bàn tròn.

A.362880    B.128800    C.246800    D.328600

Hướng dẫn giải :

Đáp án : A

Tổ 1 có tất cả 10 học sinh.Mỗi cách xếp 10 học sinh này vào một bàn tròn là một hoán vị vòng quanh của 10 phần tử nên số cách xếp thỏa mãn đề bài là:

9!= 362880 cách xếp.

Ví dụ 2 : Cuối năm học, các học sinh giỏi lớp 11A2 có tổ chức ăn liên hoan. Tổ 1 có 3 học sinh giỏi; tổ 2 có 4 học sinh giỏi; tổ 3 có 2 học sinh giỏi và tổ 4 có 3 học sinh giỏi. Hỏi có bao nhiêu cách xếp các học sinh này vào một bàn tròn?

A.10!    B.11!    C.12!    D.13!

Hướng dẫn giải :

Đáp án : B

Lớp 11A2 có tất cả số học sinh giỏi là: 3+ 4+ 2+ 3= 12 học sinh giỏi

Việc xếp 12 học sinh giỏi này vào một bàn tròn là một hoán vị vòng quanh của 12 phần tử nên số cách xếp thỏa mãn là: 11! cách xếp.

Ví dụ 3 : Tổ 4 của lớp 12A3 có 4 học sinh nữ và 5 học sinh nam . Hỏi có bao nhiêu cách xếp các học sinh này vào một bàn tròn sao cho nhóm học sinh nữ ngồi với nhau; nhóm học sinh nam ngồi với nhau.

A.1280    B.1660     C.2880    D.1860

Hướng dẫn giải :

Đáp án : C

+ Ta coi 4 học sinh nữ là một nhóm X và 5 học sinh nam là nhóm Y.

+ Số cách xếp hai nhóm X và Y vào bàn tròn là (2-1)!= 1 cách .

+ Số cách xếp 4 học sinh nữ trong nhóm X là 4!.

+ Số cách xếp 5 học sinh nam trong nhóm Y là 5!.

⇒ Có: 1. 4!. 5!= 2880 cách xếp thỏa mãn đầu bài.

Ví dụ 4 : Một hội nghị bàn tròn có ba phái đoàn: 4 người miền bắc, 3 người miền trung và 4 người miền nam. Hỏi có bao nhiêu cách xếp chỗ ngồi cho các thành viên sao cho những người có cùng miền thì ngồi gần nhau.

A.7268    B.6912    C.3286    D.4896

Hướng dẫn giải :

Đáp án : B

+ Ta coi: 4 người miền bắc là một nhóm X; 3 người miền trung là một nhóm Y và 4 người miền nam là một nhóm Z .

+ Số cách xếp ba nhóm X; Y; Z vào bàn tròn là: 2!= 2 cách.

+ Số cách xếp 4 người trong nhóm X là : 4!= 24 cách.

+ Số cách xếp 3 người trong nhóm Y là: 3!= 6 cách.

+ Số cách xếp 4 người trong nhóm Z là: 4! = 24 cách.

⇒ Số cách xếp thỏa mãn đầu bài là : 2. 24.6.24= 6912 cách.

Ví dụ 5 : Một nhóm học sinh có 6 nam và 6 nữ. Hỏi có bao nhiêu cách xếp 12 người này vào bàn tròn sao cho hai bạn cùng giới không ngồi cạnh nhau.

A.86400    B.172800    C.43200    D.Đáp án khác

Hướng dẫn giải :

Đáp án : A

+ Xếp 6 bạn nam vào 1 bàn tròn có : 5! Cách.

+ Khi đó giữa hai bạn nam có 1 vách ngăn. Có 6 vách ngăn. Xếp 6 bạn nữ vào 6 vách ngăn đó có 6! Cách.

Theo quy tắc nhân; số cách xếp thỏa mãn đầu bài là: 5!. 6!= 86400

Ví dụ 6 : Trong một buổi dự tiệc có 5 cặp vợ chồng tham gia. Hỏi có bao nhiêu cách xếp 5 cặp này vào một bàn tròn sao cho hai vợ chồng ngồi cạnh nhau.

A.96    B.192    C.768    D.384

Hướng dẫn giải :

Đáp án : C

+ Coi vợ chồng là 1 bó. Xếp 5 bó vào cái bàn tròn có 4! Cách xếp.

+ Với mỗi bó ta có thể đổi chỗ vị trí vợ; chồng cho nhau.

⇒ Với mỗi cặp vợ chồng có 2!= 2 cách xếp

Theo quy tắc nhân; số cách xếp thỏa mãn là: 4!.2.2.2.2.2= 768 cách.

Ví dụ 7 : Một nhóm văn nghệ gồm 4 bạn nữ và x bạn nam ngồi vào một bàn tròn. Biết rằng có 362880 cách xếp các bạn này vào bàn tròn. Hỏi nhóm văn nghệ này có tất cả bao nhiêu người.

A.6    B.5    C.9    D.10

Hướng dẫn giải :

Đáp án : C

+ Nhóm văn nghệ này có tất cả (4+x) bạn.

+ Số cách xếp (4 + x) bạn này vào bàn tròn là: (4+x)!

Theo đầu bài ta có: (4+x)! = 362880= 9!

⇔ 4 + x= 9 ⇔ x= 5

⇒ Nhóm văn nghệ có 5 bạn nam nên cả nhóm này có 4 + 5= 9 bạn

Ví dụ 8 : Lớp 10A1 tổ chức một buổi khen thưởng. Biết tổ 1 có 3 người được khen thưởng; tổ 2 có 2 người; tổ 3 có 4 người và tổ 4 có x người.Xếp những người này vào một bàn tròn và các bạn cùng tổ ngồi liền kề với nhau. Biết có 10368 cách xếp thỏa mãn. Tìm x ( biết x>0)?

A.1     B.2    C.3    D.4

Hướng dẫn giải :

Đáp án : B

+ Số cách xếp 4 tổ vào 1 bàn tròn là 3!.

+ Tổ 1 có 3 bạn ngồi liền kề với nhau. Hoán đổi vị trí của 3 bạn này có 3! Cách.

+ tổ 2 có 2 bạn ngồi liền kề với nhau. Hoán đổi vị trí của 2 bạn này có 2! Cách.

+ Tổ 3 có 4 bạn ngồi liền kề với nhau. Hoán đổi vị trí của 4 người này có 4! Cách.

+ Tổ 4 có x bạn ngồi liền kề với nhau. Hoán đổi vị trí của x người này có x! cách.

Theo quy tắc nhân; số cách xếp thỏa mãn là:

3!. 3!.2!. 4!.x!= 10368

⇔ x!= 6 ⇔ x= 2

BÀI TẬP

Câu 1: Có bao nhiêu cách sắp xếp 6 bạn nam và 4 bạn nữ vào ngồi 1 dãy ghế hàng ngang có 10 chỗ ngồi?

ĐÁP ÁN: 10!

Câu 2: Sắp xếp 5 bạn học sinh A, B, C, D, E vào ngồi 1 chiếc ghế dài 5 chỗ ngồi. Có bao nhiêu cánh sắp xếp sao cho bạn C luôn ngồi chính giữa?

ĐÁP ÁN: 24

Câu 3: Sắp xếp 5 bạn học sinh A, B, C, D, E vào ngồi 1 chiếc ghế dài 5 chỗ ngồi. Có bao nhiêu cánh sắp xếp sao cho bạn A và B luôn ngồi hai đầu ghế?

ĐÁP ÁN: 12

Câu 4: Sắp xếp 5 bạn học sinh A, B, C, D, E vào ngồi 1 chiếc ghế dài 5 chỗ ngồi. Có bao nhiêu cánh sắp xếp sao cho bạn A và D luôn ngồi cạnh nhau?

ĐÁP ÁN: 48

Câu 5: Sắp xếp 5 bạn học sinh A, B, C, D, E vào ngồi 1 chiếc ghế dài 5 chỗ ngồi. Có bao nhiêu cánh sắp xếp sao cho bạn A và D luôn không gồi cạnh nhau?

ĐÁP ÁN: 72

Câu 6: Có 3 viên bi trắng khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Hỏi có bao nhiêu cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng một màu ở cạnh nhau?

ĐÁP ÁN: 103680

Câu 7: Cô dâu chú rễ mời 6 người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu cách sắp xếp sao cho cô dâu chú rễ luôn đứng cạnh nhau?

ĐÁP ÁN: 2.7!

Câu 8: Cô dâu chú rễ mời 6 người ra chụp ảnh kỉ niệm, người thợ chụp hình có bao nhiêu cách sắp xếp sao cho cô dâu chú rễ luôn đứng cạnh nhau và luôn đứng giữa bức ảnh?

ĐÁP ÁN: 2.6!

Câu 9: Trên giá sách muốn xếp 20 cuốn sách khác nhau . Có bao nhiêu cách sắp xếp sao cho tập 1 và tập 2 không đặt cạnh nhau?

ĐÁP ÁN: 20!-2!19!

Câu 10: Với các chữ số 1, 2, 3, 4,5, 6 có thể lập được bao nhiêu số có 8 chữ số, trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng 1 lần?

ĐÁP ÁN: 6720

Câu 11: Nam có 4 cái quần dài giống nhau, 6 cái áo trắng như nhau, 5 cái áo sơ mi giống nhau. Nam treo hết quần áo ở trên thành 1 hàng thẳng trong tủ treo đồ. Hỏi có bao nhiêu cách sắp xếp?

ĐÁP ÁN:

Câu 12: Có 10 vị khách xếp vào một bàn tròn 10 chỗ thì có bao nhiêu cách?

ĐÁP ÁN: 9!

Câu 13: Một nhóm có 5 bạn nam và 5 bạn nữ xếp thành 1 hàng ngang. Tính số cách sắp xếp để cho các bạn nam nữ ngồi xen kẽ với nhau?

ĐÁP ÁN: 2.(5!)²

II. Chỉnh hợp

a) Định nghĩa:

– Cho tập hợp A gồm n phần tử (n ≥ 1).

Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

b) Số các chỉnh hợp:

– Kí hiệu: A_n^k là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n).

– Định lý:

– Lưu ý: Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó. Vì vậy, ta có: P_n = A_nⁿ

Ví dụ 1:

Có bao nhiêu số tự nhiên gồm $4$chữ số khác nhau được lập thành từ các chữ số $1,2,3,4,5,6,7$?

Hướng dẫn:

Mỗi số tự nhiên gồm $4$ chữ số khác nhau được lập bằng cách lấy $4$ chữ số từ tập $A=\left\{1;2;3;4;5;6;7\right\}$ và xếp chúng theo một thứ tự nhất định.

Mỗi số như vậy được coi là một chỉnh hợp chập $4$ của $7$ phần tử.

Vậy số các số cần tìm là  ${\mathrm{A74}}^{}=\mathrm{840\; số.}$

 BÀI TẬP

Câu 1: Một nhóm có 4 bạn A, B, C, D. Hãy tính số cách chọn ra 3 bạn để phân công làm trực nhật: Một bạn quét nhà, một bạn lau bảng và một bạn kê bàn ghế.

ĐÁP ÁN: A₄³   

Câu 2: Lập được bao nhiêu số tự nhiên có năm chữ số khác nhau từ các chữ số 1,2, …9?

ĐÁP ÁN: A⁵₉

Câu 3: Trong mặt phẳng cho một tập hợp gồm 6 điểm phân biệt. Có bao nhiêu véc tơ khác véc tơ o có điểm đầu và điểm cuối thuộc tập hợp này.

ĐÁP ÁN: A₆²

Câu 4: Có bao nhiêu số có 3 chữ số khác nhau có thể lập từ các chữ số 0; 2; 4; 6; 8

ĐÁP ÁN: – Chữ số hàng trăm khác 0 nên có 4 cách chọn từ 4 số 2; 4; 6; 8. Hai chữ số còn lại có A₄²  cách chọn. Vậy có 4.A₄² =48 số

 III. Tổ hợp

a) Định nghĩa:

– Giả sử A có n phần tử (n ≥ 1). Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).

– Quy ước: Tổ hợp chập 0 của n phần tử là tập rỗng.

b) Số các tổ hợp:

– Kí hiệu C_n^k là số các tổ hợp chập k của n phần tử (0 ≤ k ≤ n).

– Định lý:

c) Tính chất của các số C_n^k

– Tính chất 1:

    C_n^k = C_n^{n – k} (0 ≤ k ≤ n)

– Tính chất 2:

Ví dụ:

Một bàn học sinh có $3$nam và  nữ. Có bao nhiêu cách chọn ra  bạn để làm trực nhật?

Hướng dẫn:

Mỗi cách chọn ra  bạn để làm trực nhật là một tổ hợp chập  của  phần tử.

Vậy số cách chọn là: ${\mathrm{C52}}_{}=$ (cách) 

 BÀI TẬP 

Câu 1: Một nhóm có 4 bạn A, B, C, D. Hãy tính số cách chọn ra 3 bạn để thành lập một tổ trực nhật ( không có sự phân công nhiệm vụ cho từng bạn)?

ĐÁP ÁN: C₄³

Câu 2: Trong mặt phẳng cho một tập hợp gồm 6 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Lập được bao nhiêu đoạn thẳng và tam giác có các đỉnh thuộc tập hợp này?

ĐÁP ÁN: C₆²    ; C₆³

BÀI TẬP TỔNG HỢP:

1. Có bao nhiêu cách chọn 4 bạn từ 6 bạn để lập 1 danh sách ban cán sự lớp ?
2. Một lớp có 40 học sinh gồm 25 nam và 15 nữ. chọn ra 3 em đi thi học sinh giỏi thì có bao nhiêu cách chọn?
3. Có bao nhiêu cách xếp khác nhau cho 6 người ngồi vào 3 chỗ trên một bàn dài?
4. Có 7 bông hoa khác nhau cắm vào 3 lọ khác nhau. Hỏi có bao nhiêu cách cắm 3 bông hoa vào 3 lọ đã cho ( mỗi lọ cắm 1 bông)?
5. Có bao nhiêu cách mắc nối tiếp 4 bóng đèn được chọn từ 6 bóng đèn khác nhau?
6. Một hộp đựng 5 viên bi xanh và 7 viên bi vàng. Có bao nhiêu cách lấy ra 6 viên bi bất kì?
7. Có bao nhiêu cách lấy ra 2 con bài từ cỗ bài tú lơ khơ gồm 52 con?
8. Trong một cuộc thi có 15 người tham dự, giả thiết không có hai người nào bằng điểm nhau. Nếu kết quả cuộc thi là việc chọn ra các giải nhất, nhì, ba thì có bao nhiêu kết quả có thể xảy ra?
9. Có 100 tờ vé số đánh số thứ tự từ 1 đến 100 phát cho 100 người. Kết quả có 4 giải nhất, nhì, ba, tư. Hỏi có bao nhiêu kết quả có thể sảy ra biết rằng người giữ số 20 đạt giải nhất?
10. Có 15 đội bóng đá thi đấu theo thể thức vòng tròn tích điểm. Hỏi cần phải tổ chức bao nhiêu trận đấu?
11. Có bao nhiêu cách cắm 3 bông hoa giống nhau vào 5 lọ khác nhau ( mỗi lọ cắm không quá 1 bông)?
12. Trong mặt phẳng cho tập hợp P gồm 2019 điểm phân biệt. Lập được bao nhiêu đoạn thẳng mà có hai đầu mút thuộc tập P?
13. Trong mặt phẳng có tập hợp P gồm 7 điểm ( trong đó không có 3 điểm nào thẳng hàng). Hỏi có bao nhiêu tam giác có 3 đỉnh thuộc P?
14. Một tổ có 10 người gồm 6 nam và 4 nữ. Cần lập một đoàn đại biểu gồm 5 người. Hỏi có tất cả bao nhiêu cách lập?
15. Một tổ có 10 người gồm 6 nam và 4 nữ. Cần lập một đoàn đại biểu gồm 5 người trong đó có 3 nam và 2 nữ. Hỏi có tất cả bao nhiêu cách lập?
16. Có 16 đội bóng đá tham gia thi đấu.  Hỏi cần tổ chức bao nhiêu trận đấu sao cho hai đội bất kỳ đều gặp nhau dúng 1 lần?

Câu số	1	2	3	4	5	6	7	8	9
Đáp án	360	9880	120	210	360	C612	C252	2730	941094

 

Câu số	10	11	12	13	14	15	16	17	18
Đáp án	C215	10	C22019	35	252	C36 . C 24	C216

Gia sư online